U okviru predmeta Geometrija i vizuelizacija slobodnih formi, za ispitni rad, po slobodnoj volji izabran je projekat The Bobst Pixel Veil u sklopu zgrade biblioteke univerziteta u Njujorku ( Elmer Holmes Bobst Library), čiju realizaciju je izveo tim arhitekata Joel Sanders Architect, 2012. godine.
Prilikom odabira ovog projekta, bilo je u vidu korišćenje alata koji dozvoljavaju parametarsko modelovanje, kako bi se jedan element – panel reprodukovao sa sličnim parametrima, ali drugačije forme. Bilo je neophodno prvo analizirati projekat tima arhitekata Joel Sanders-a, kako bi bila moguća njegova reprodukcija. Napominjem, da cilj ovog rada, nije da se reprodukuje projekat u komercijalne svrhe, već da se primeni logika koja je nastala pri njegovoj izradi.
Način na koji se ravijao rad je kompleksan, te nije prikladno u ovom formatu pokazivati proces, tako da ću pokušati u daljem tekstu da definišem samo finalni rezultat. Finalni rezultat, kao takav, bi bio propraćen prezentacijom same definicije, koja je ključni deo rada, i koja je sastavljena u programskom okruženju namenjenom za parametarsko modelovanje.
VIZUELIZACIJA
Iako nije tema rada, bio bi greh ne prezentovati već gotovu geometriju na ‘adekvatan’ način. Nakon dužeg vremena optimizovanja definicije, da bi se jednim klikom dobio finalni rezultat panela, prosto je zadovoljstvo. Tako da umesto da kreiram više slika koje predstavljaju geometriju i kontekst u kome se ona nalazi, u različitim uglovima i osvetljenjem, što je dug proces, opredelio sam se za interaktivnu vizuelizaciju.
Početna ideja se javila u procesu izrade ovog rada, jer sam imao veliku želju i iskušenje da doživim unutrašnjost ovakvog atrijuma. Zbog vremena koje sam dodelio ovom zadatku, najoptimalnije rešenje je bila vizuelizacija sa uglom gledanja od 360 stepeni. Prvobitno sam želeo da se njena realizacija odvija u proširenoj realnosti, u okviru android uređaja korišćenjem informacija iz senzora ubrzanja da se menja ugao gledanja. Na žalost, usled nedostatka vremena, projekat je ostao na platformi koja je naizgled optimizovana za pregled informacija tog formata.
Kontekst vizuelizacije je sveden, zasniva se uglavnom na prezentaciji dobijenih panela u zatvorenom prostoru.
Klikni na animaciju kako bi se učitala vizuelizacija od 360 stepeni.(Navigacija levi klik miša/strelice, +/- promena fokalne dužine – ne funkcioniše u fullscreen modu)
GEOMETRIJA
Neophodno je izmodelovati jedan panel odgovarajućih dimenzija, koji bi bio nasumično segmentisan na podeoke koji bi bili nasumično prisutni, kao i horizontalne prečke koje se takođe nasumično pojavljuju kroz panel. U oviru takvog panela, potrebna je organizovana vertikalna podela na kolona i vertikalnih gredica. Potrebna je i izrada nosača, tj. noseće grede koja nosi panel kao i ankeri za vezivanje panela sa nosećom gredom.
Da bi to postigli pre svega moramo izabrati softversko okruženje koje je optimizovano za naše potrebe. Nakon toga treba razviti logiku razbijanja date forme, i izanalizirati je od samog početka kao i međuzavisnost svih elemenata u njemu.
Da bih sveo čitav proces razvijanja logike koje je bilo neophodno u procesu kreiranja ovog rada, napravljena je animacija propraćena zvukom koja govori više o tome, kao i o mom stanju svesti u datom trenutku.
Klikni na sliku, da bi započela animacija sa zvukom!
Međutim, pošto animacija ne govori ništa konkretno, u daljem tekstu možete naći detaljnije uputstvo za izradu ovakvog panela.
Proces realizacije finalne geometrije može se ispratiti na sledećem dijagramu.
Napomena: dijagram je sveden šematski prikaz, te su izostavljeni pojedini koraci, kao i input podaci, zbog njihove veličine i brojnosti.
01. Linija
Celokupna geometrija panela u daljoj definiciji zavisi od jedne linije. Od nje počinje generisanje ostale forme. Zadajemo po z-osi visinu liniji, odnosno kasnije visini panela.
02. Segmentisanje linije – broj segmenata
Da bi se linija segmentisala nasumično, neophodno je dobro poznavati softversko okruženje. Alat koji sam koristio pri izradi ovog rada je zasnovan na konceptu lista i grana, nalik matricama u matematici odnosno iz programiranja teorija grafova gde su grane prikazane kao usmereni graf sa predifinisanom definicijom stabla.
Dakle, za nasumičnu segmentaciju linije, neophodne su nam pojedine informacije. Visina linije, broj segmenata, odnosi između segmenata.
Visinu linije smo dobili u prethodnom koraku, pa treba da pretvorimo njenu visinu u veličinu u domenu od 0 do 1, gde nula predstavlja minimalnu visinu, a jedan maksimalnu. Potom treba da uvrstimo broj segmenata (1,1,1,1,1) i takođe ih uvrstimo u domen od 0 do 1, tako što ćemo sabrati svaki sa svakim i svaki broj podeliti sa tim rezltatom. Dobili smo pet jednakih segmenta. A ako promenimo odnose između brojeva (2,4,1,5,4,1), dobijamo različite međuodnose koji će biti dodeljeni za segmentaciju linije šest puta. Ti input podaci, zapravo neće biti predodređeni u ovom radu, već nasumično izabrane vrednosti u određenom domenu (npr. od 12 do 70) (25,53,62,17,13,22,41,33,59 itd.).
03. Pozicioniranje linija u raster
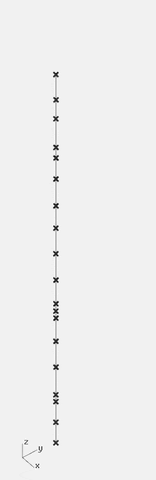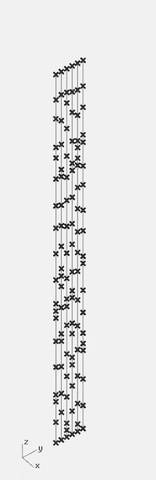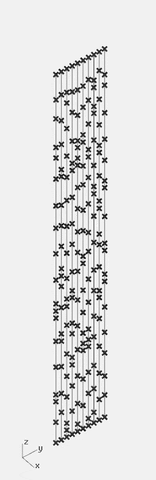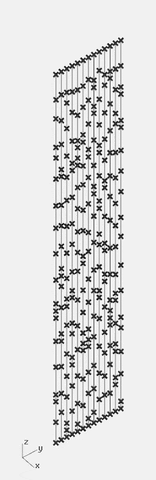
Pozicioniranje linija u raster po y-osi, koji kasnije treba da oformi kolone na određenoj udaljenosti.
Kako smo segmentisali liniju u prethodnom koraku, isti postupak je i ovde. Ali umesto da generišemo seriju brojeva za svaku liniju, mi generišemo seriju serija, odnosno stablo se grana. Sada umesto jedne serije (2,4,1,5,4,1), imamo toliko serija koliko kolona želimo da imamo. Npr. (2,4,1,5,4,1)(2,4,1,5,4,1)(2,4,1,5,4,1)(2,4,1,5,4,1), dobili smo četiri jednako segmentisane linije. Ali nama je cilj nasumičnost, pa menjamo nasumično raspored između brojeva u serijama (2,1,4,5,4,1)(2,4,1,5,4,1)(2,1,4,1,4,5)(5,4,4,5,1,1). Isto važi gore pomenuto, serije su nasumično izabrane vrednosti. Dakle za 13 kolona treba nam 13 serija brojeva. Svaka linija treba da bude sastavljena od 20 segmenata, 20 segmenata u svakoj seriji.
04. Varijacija segmenata linija
Imamo željenu visinu kolona, broj kolona, broj segmenata i definisan i odnosi između njih. Nasumično menjamo redosled brojeva u okviru serija, što nam daje moć upravljanja nad svim elementima panela.
05. Širina kolona
Kontrola nad razmakom između linija, daje nam kasnije kontrolu nad širinom kolona u panelu, tako što svaka linija ostavlja dovoljno mesta za prethodnu liniju, kao i vertikalnu gredicu koja treba da se nalazi između njih.
06. Broj segmenata – sve linije
Isto kao i drugi korak, samo što ovde nemamo jednu seriju brojeva za jednu liniju već 13 serija za 13 linija, u kojima se broj brojeva, odnosno dužina serija povećava kao što je prikazano na slici.
07. Vertikalne gredice
Pošto smo ostavili u petom koraku mesta za vertikalne gredice, neophodno je da ih pozicioniramo na ta mesta. Pravimo seriju od 12 (između kolona)+2 (na krajevima niza kolona) linija da popunimo razmake između kolona, tako što koristimo istu liniju iz prvog koraka. Nakon toga zadajemo joj širinu, tj. linije postaju površine, ali tako da je međusobno zavisna od širine kolona, da ne bi došlo do preklapanja geometrije.
08. Kolone
Imamo definisane vertikalne gredice, sada zadajemo širinu kolonama, tako što linija postaje površina. Pošto su vertikalne gredice i kolone zavisne, kako povećavamo jednu promenljivu, tako utičemo na drugu promenljivu.
09. Okvir
Pošto smo definisali najosnovnije parametre potrebne panel, u ovom koraku definišemo okvir, preko kojeg se panel vezuje za međuspratnu konstrukciju, ili samo iz estetskih razloga.
Okvir dobijamo opet od početne linije, tako što selektujemo njene krajeve, dupliramo tačke na drugi kraj panela, i međusobno ih povežemo linijama tako da dobijemo linije iznad i ispod panela. Nakon toga zadamo širinu po z-osi.
10. Nasumična selekcija podeoka
Nasumična selekcija podeoka, tako da jedne podeoke isključuje iz finalne geometrije, a druge ostavlja. Paneli koji su ‘preživeli’ selekciju oni čine finalnu geometriju. Međutim pošto je selekcija nasumična, a ne svaki drugi panel odstranjen, stvaraju se međusobno bliski paneli, što je prepreka za finalnu geometriju zbog potreba fabrikacije. Može se smatrati da je ovaj deo definicije greškom. Uprkos tome, opredelio sam se za ovaj korak, jer dobijamo veću nasumičnost. Dobijene panele koji imaju susedno od sebe još jedan ili dva panela, pripajamo tako da dobijemo jedan veći panel u koloni, koji je istih dimenzija kao prethodna dva, odnosno tri panela. Tako dobijamo veće odnose između veličina panela, što je u početnim serijama brojeva teško generisati nasumično brojeve u određenom domenu, a da njihov prosek ne bude sličan.
11. Varijacija podeoka, odnosno perforacija
Nakon što smo odstranili potreban deo podeoka, odnosno dobili potreban deo perforacija u panelu, možemo da izvršimo njihovu varijaciju u svakom trenutku, zahvaljujući postupku koji smo definisali u četvrtom koraku.
12. Horizontalne prečke
Nakon izvršenja selekcije panela, imamo pristup listi panela koji nisu prošli selekciju. Idealan način da se primeni modifikovanje već gotove geometrije, inače u suprotnom morali bi da postavljamo nasumično prečke u perforacije, koje moramo pre toga da definišemo i izdimenzionišemo. Zahvaljujući gotovoj listi panela, izvršimo pripajanje susednih panela, ali tako da ne obrišemo linije između njih kao u desetom koraku, jer nam zapravo samo te linije i trebaju. Njih ćemo dobiti tako što izvršimo selekciju unutrašnjih linija svih podeoka, tako da ako ima bar dva susedna panela koja nisu prošla selekciju stvoriće se opcija da se napravi jedna prečka. Od svih dobijenih unutrašnjih linija pravimo prečke tako što liniji zadajemo širinu, i repozicioniramo na svoje početno mesto. Tako smo dobili zavisnost između svega. Kako smanjimo broj perforacija, manje su šanse da će se horizontalne prečke pojaviti. Nakon toga, možemo i da izvršimo nasumičnu selekciju prečki, jer ako želimo otvoreniji panel, broj prečki bi bio previsok.
13. Varijacija horizontalnih prečki
Pošto smo izabrali potreban broj prečki u panelu, možemo nasumično da menjamo njihovu poziciju, koja zavisi od preostalih prečki. Odnosno, variramo koje će prečke biti odsutne, odnosno prisutne u finalnoj geometriji.
14. Debljina panela
Dobili smo finali panel, radi bolje vizuelizacije zadajemo mu debljinu po trećoj, x-osi.
15. Širina noseće grede
Odredili smo izgled panela. Dalji rad se odnosi samo na noseću konstrukciju panela. Definišemo širinu noseće grede, tako što izvršimo selekciju tačaka početne linije iz prvog koraka, repozicioniramo tačke tako da dodamo visinu okvira iz devetog koraka, i spojimo linijom tako da se linije nalaze sa leve i desne strane panela. Pošto smo to uradili, treba linijima zadati širinu, odnosno dobijamo širinu noseće grede.
16. Ankeri i njihova varijacija
Do sada smo se oslanjali uvek na početnu geometriju sa početka definicije jer je lakše, između ostalog, izršiti njihovu selekciju. Međutim kada definija postane dublja, moramo se osloniti na dobro organizaciju stabla, kako bi mogli i dalje da imamo kontrolu nad njim, samim tim i kontrolu selekcije i modifikacije iste.
Da bi definisali ankere koji vezuju panel i noseću gredu, neophodno je izvršiti selekciju svih nasumično selektovanih panela u koloni koji su prošli selekciju i prošli susedno pripajanje. Potrebno je izvršiti selekciju prve i poslednje kolone panela, odnosno grane stabla i rotirati je za 90 stepeni oko z-ose. Pošto je od samog početka definicija tako definisana, da je jedna kolona jedna serija brojeva, tj. jedna grana, pruža nam mogućnost selekcije kolone, odnosno panela koji se u njoj nalaze.
Npr. (0,0,1,0)(0,0,1,1)(0,0,1,2)(0,0,1,3)…(0,0,1,13), izvršimo selekciju prve grane, znajući da je ona prva kolona (0,0,1,0), obrnemo listu (jer je broj kolona promenljiva, a ne može se selektovati poslednja) (0,0,1,13)(0,0,1,12)(0,0,1,11)…(0,0,1,0) i opet izvršimo selekciju prve grane, odnosno prve kolone (0,0,1,13). Uspešno smo izvršili selekciju prve i poslednje grane (0,0,1,0)(0,0,1,13). I pošto je sve zavisno, ankeri će biti biti prisutni samo tamo gde su prisutni i podeoci u koloni, kako bi mogli da se vežu za njih.
17. Debljina noseće konstrukcije
Zadajemo debljinu noseće grede posebnom promenljivom, dok debljina ankera ista kao i debljina podeoka u panelu, odnosno panel.
Kako se debljina noseće grede menja, tako se pomeraju ankeri zajedno sa njim, da bi se očuvala veza između grede i panela.
18. Finalna geometrija
Sve promenljive su određene kako nama odgovara. Da bi izvršili reprodukciju sličnih panela, različitog izgleda, treba samo da menjamo promenljive poput varijacije panela, varijacije prečki i slično.
Međutim ništa nas ne sprečava da u ovom trenutku, promenimo možda visinu, ili možda dodamo još jednu kolonu, ili pak uklonimo okvir, ili ako nisam siguran u broj horizontalnih prečki, da dodamo još jednu za svaki slučaj, ili možda povećamo noseću gredu jer nam statika ne valja, ili, ili možda ne.
Definicijia
Prva verzija definicije
Kao što je ranije napomenuto, problem dobijanja finalne geometrije se može parametarskim putem rešiti na mnogo načina. Jedan od načina koji je izabran za definisanje geometrije je objašnjen gore u tekstu.
low res. prikaz definicije – verzija 1
Druga verzija definicije
U odnosu na taj način, panel se mogao segmentisati od jedne površine na određene delove, tako što dimenzije segmenata ne bi bili unošeni direktno, već odnosi broja segmentacija u odnosu na ukupnu dimenziju panela bi bili procentualno izraženi. Međutim iako je taj postupak logični pristup, veoma je lakše softverskom okruženju da kalkuliše od prostije geometrije promene, u odnosu na površinu, ili pak kompleksnije forme. Time dobijamo brži interaktivni pristup menjanju promenljivih, dok u drugom načinu zbog određenih komponenti, koje se ne mogu izbeći, povećava se vreme kalkulacije geometrije.
low res. prikaz definicije – verzija 2
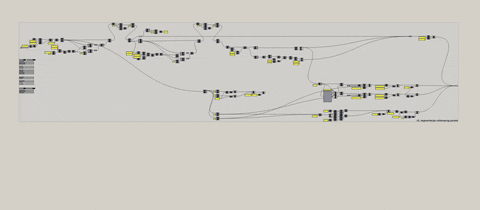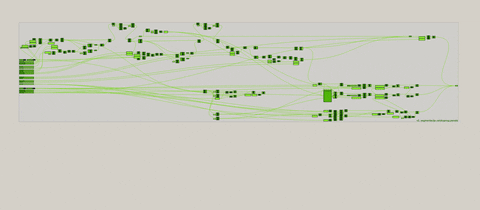
Input podaci preko android uređaja
Kako je prva verzija definicije je izabrana za dalji rad, ideja da se parametri tj. promenljive menjaju drugim putem, van programskog okruženja, je proistekla iz potrebe da se rad dalje prezentuje. Tako je napravljena još jedna verzija prve verzije definicije, gde se input podaci zadaju van okvira softverskog okruženja, već input informacije dolaze sa android uređaja. Isto tako bilo je moguće, koristiti mnogobrojne senzore korišćenjem mikro-kontrolera za promenu parametara, ali taj korak je preskočen, jer je suvišan za ovaj rad.
Pre svega je potrebno optimizovati interfejs u okviru android uređaja da bi bila i dalje omogućena veza sa definicijom. Input parametre zadajemo preko slajdera koji ima određene vrednosti i zamenjujemo sa slajderima u originalnoj definiciji. Da bi se ovo realizovalo, korišćen je OSC (Open Sound Control) protokol, preko kojeg android uređaj komunicira i šalje podatke računaru na kome je aktivan kod.
low res. prikaz definicije, verzija 1 – input preko android uređaja
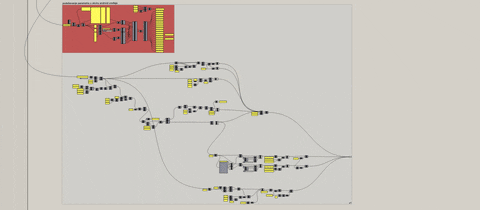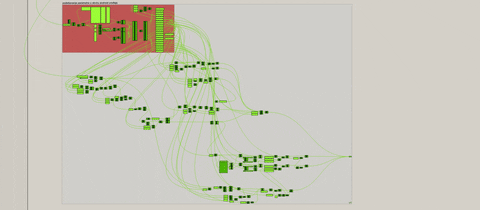
Kako bi sve finkcionisalo neohodno je ispoštovati određene korake, ali pošto to nije glavna tema rada, samo ću demonstrirati samu aplikaciju različitih inputa.
Klikni na animaciju, kako bi započeo video. Kratka (i veoma loša) demonstracija okruženja.
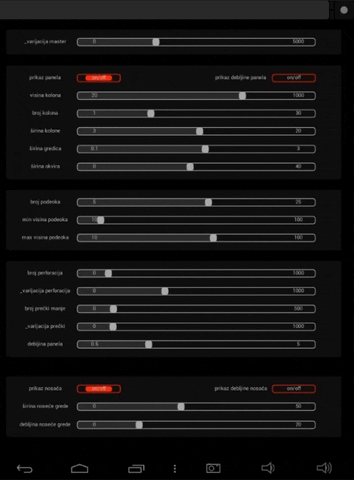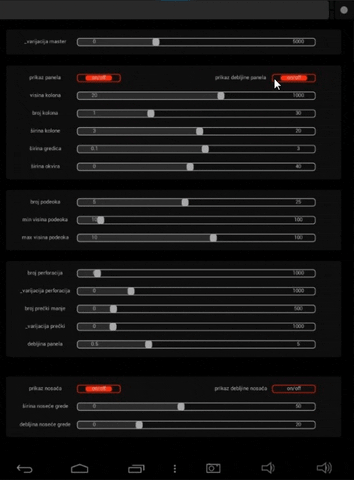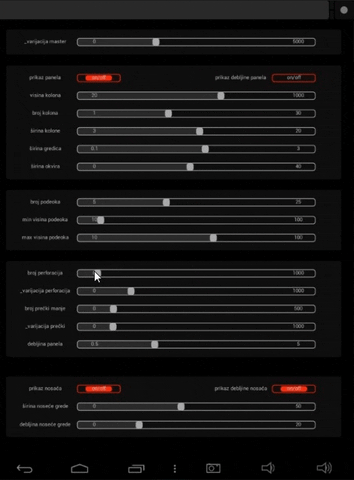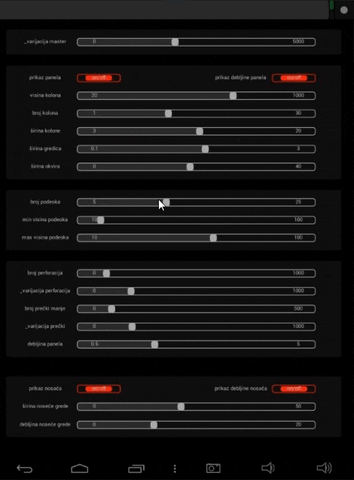
High Res. prikaz definicije možete naći na sledećem linku za download, zbog nemogućnosti pretraživača da prikaže prikaz definicije zbog njene veličine.
DIGITALNA FABRIKACIJA
Na samom kraju, šteta je nerealizovati rad u realnom okruženju. Da bi se definicija odnosno panel izbacio iz digitalnog okruženja, neophodno je ispoštovati da se elementi panela, tj. njihova geometrija ne poklapa. Pošto smo to uspeli da uradimo, za digitalnu fabrikaciju je odlučeno da se koristi CNC mašina sa laserskom glavom, koja je optimizovana za rad nad pločastim elementima. Sledeći korak je izvoženje svih linija panela, ne finalne geometrije, vodeći računa da nema linija koje se preklapaju, i pozicioniranje na dizmenzije materijala koji je spreman za sečenje.
low res. prikaz definicije – verzija 1, izdvojena zelena grupa komponenti je zaslužna za fabrikaciju panela.
Alati korišćeni za izradu ovog rada
- Rhinoceros 5 (modelovanje);
- Grasshopper for Rhinoceros (parametarsko modelovanje, priprema za digitalnu fabrikaciju, animacija);
- Ghowl for Grasshopper (android veza);
- TouchOSC (android interfejs);
- V-ray for Rhinoceros (vizuelizacija);
- Pano2VR (360° okruženje);
- Adobe Photoshop (postprodukcija);
- Grasshopper (animacija);
- Adobe Premiere Pro (montaža);
- Adobe After Effects (vizuelni efekti)
- AutoCad (digitalna fabrikacija)
- I mnogi drugi, manje značajni alati prilikom izrade projekta.
Link za skidanje celokupne definicije možete naći ovde.
Hvala na pažnji,
Ferenc Andrej.
