U ovoj fazi istraživanja prikazuje se primena prethodno definisane metode na konkretnim algoritmima slaganja Rubikove kocke. Cilj je da se ispita kako se razvijeni sistem ponaša u praksi – da li formirane strukture uspešno prenose informaciju o sekvenci poteza i da li su čitljive drugim korisnicima.
Proces započinje jednostavnijim primerom, koji služi za proveru osnovne funkcionalnosti i odnosa između kretanja, rotacije i formirane površine. Nakon toga biće prikazano nekoliko kompleksnijih primera, u kojima se ispituje sposobnost sistema da održi jasnoću i logiku pri većem broju poteza i složenijim kombinacijama.
Na kraju, kroz anketno ispitivanje drugih korisnika, analiziraće se da li je vizuelna forma zaista razumljiva i da li omogućava delimičnu ili potpunu rekonstrukciju algoritma. Ovaj korak predstavlja završnu proveru hipoteze i osnov za zaključak istraživanja.
Primer 1 – Osnovni algoritam (L, R, U, D):
U prvom primeru prikazan je osnovni niz poteza: L (left), R (right), U (up) i D (down), gde je smer rotacije redom: CW(clockwise), CW(clockwise), CCW(counterclockwise), CCW(counterclockwise). Ovaj niz odabran je kako bi se ispitao osnovni princip funkcionisanja metode na jednostavnijoj sekvenci kretanja.
Da bi se formirala odgovarajuća slobodna forma, algoritam je izveden obrnuto na Rubikovoj kocki, kao što su i pravci kretenja obrnuto (D, U, R, L), polazeći od već složene kocke. Smerovi rotacije su takodje obrnuto radjeni za svaki korak pojedinačno (CCW, CCW, CW, CW). Na taj način bilo je moguće precizno pratiti redosled promena boja koje se javljaju tokom svakog poteza. Boje su zatim iskorišćene kao referenca za formiranje geometrijske strukture, čime je svaka promena na kocki dobila svoj vizuelni i prostorni ekvivalent. Rezultat ovog procesa je slobodna forma koja sledi logiku kretanja tačke u prostoru i odražava ritam algoritma.


Fotografija 1: Dobijena forma prikazana iz dve perspektive
Izvor: autorska fotografija
Video 1: Sinhronizovano formiranje oblika sa pokretima Rubikove kocke
Izvor: autorski video
Primer 2 – Algoritam (R, U, D, L, R, R)
Drugi primer prikazuje složeniju sekvencu poteza: R, U, D, L, R, R, uz prateće smerove rotacije: CW, CW, CCW, CCW, CW, CW.
Za razliku od prethodnog, jednostavnijeg primera, ovde se ispituje ponašanje sistema pri većem broju poteza i čestim promenama smera rotacije. Time se analizira kako se geometrijska forma razvija kada se sekvenca poteza ubrzava.
Kao i u prethodnom primeru, algoritam je izveden unazad na već složenoj kocki, kako bi se precizno pratile promene boja i orijentacije svake površine. Pravac kretanja je izveden koracima: R, R, L, D, U, R, dok su smerovi rotacije: CCW, CCW, CW, CW, CCW, CCW. Dobijeni podaci korišćeni su za generisanje slobodne forme koja pokazuje izraženiju dinamiku i složeniju prostornu logiku u odnosu na prethodni model.

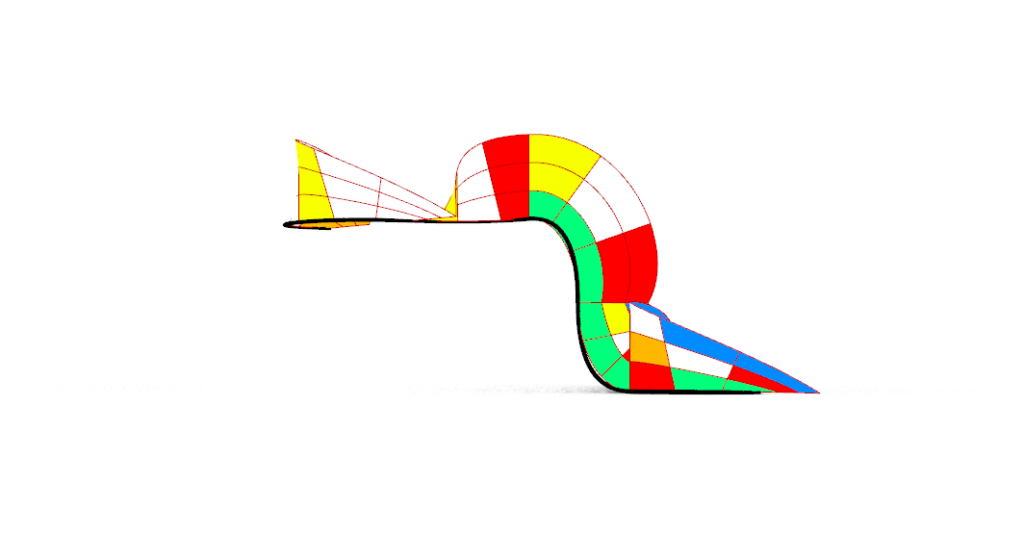
Fotografija 2: Dobijena forma prikazana iz dve perspektive
Izvor: autorska fotografija
Primer 3 – Algoritam (U, D, R, D, L, U, D, R, L)
Treći primer prikazuje najkompleksniji niz poteza u okviru istraživanja: U, D, R, D, L, U, D, R, L, uz prateće smerove rotacije: CW, CCW, CCW, CW, CW, CW, CCW, CW, CCW.
Ovaj algoritam je odabran kako bi se proverilo da li sistem ostaje konzistentan i čitljiv pri većem broju uzastopnih transformacija, promena smera i povratnih poteza. Naglasak je stavljen na sposobnost forme da zadrži kontinuitet i logičku povezanost, uprkos složenoj dinamici kretanja u prostoru.
Kao i kod prethodnih primera, algoritam je izveden na već složenoj kocki u obrnutom redosledu, što je omogućilo praćenje svih promena boja i prostorne orijentacije. Na osnovu tih promena formirana je složena slobodna površina, koja vizuelno prikazuje ritam, kontraste i međusobne odnose poteza.
Dobijeni rezultat pokazuje znatno izraženiju prostornu složenost i dinamički karakter forme, čime se potvrđuje mogućnost metode da vizualizuje i duže algoritme bez gubitka estetske ili informativne vrednosti.


Fotografija 3: Dobijena forma prikazana iz dve perspektive
Izvor: autorska fotografija
Zaključak istraživanja
Rezultati faze III pokazali su da se razvijeni sistem uspešno primenjuje i na složenije algoritme, zadržavajući čitljivost i logiku sekvence. Vizuelne forme potvrđuju sposobnost da prenesu informaciju o potezima kroz geometrijsku strukturu. Time je potvrđena hipoteza da se algoritam Rubikove kocke može prevesti u estetski i informativan prostorni zapis.

