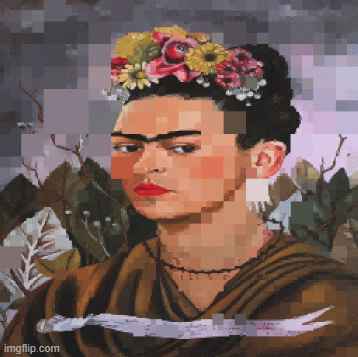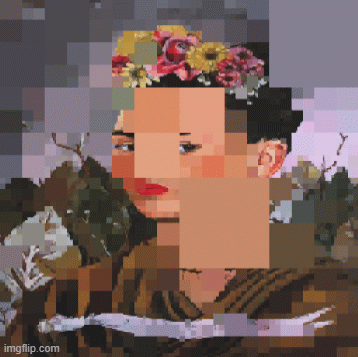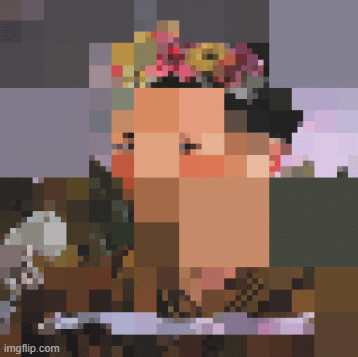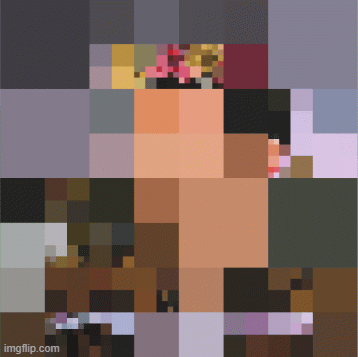Analiza i komparacija rezultata Grasshopper/Python
Za istraživanje su odabrana dva poznata umjetnička djela – „Dama sa hermelinom“ Leonarda da Vinčija i autoportret Fride Kalo. Razlog za ovakav izbor leži u njihovim različitim koloritskim osobinama: u prvom slučaju dominira tamna pozadina sa ujednačenim tonovima i bez izraženih prelaza između nijansi, dok drugo djelo karakteriše bogatiji i raznovrsniji kolorit. Upravo zbog tog kontrasta u koloritu, ova dva djela uzeta su kao osnov za posmatranje i analizu.
Autoportret Fride Kalo:

Istraživanje je obuhvatilo tri nivoa iteracija – 3, 5 i 7. U Python-u se jasno uočava da povećanjem broja iteracija raste i stepen detaljnosti, jer se proces rekurzije ponavlja više puta. Paralelno, viši prag homogenosti (threshold) dovodi do većih i ujednačenijih kvadrata. Kod iteracije tri kvadrati su skoro iste veličine pri nižim granicama homogenosti, pa je lik teško prepoznati. Sa pet iteracija slika postaje osjetno razloženija, naročito pri nižim pragovima, dok se prepoznatljivost gubi za granicu homogenosti 30. Najveći broj iteracija – sedam, daje najdetaljniji prikaz – oblik ostaje čitljiv sve do praga 30, a tek tada dolazi do gubitka jasnoće, ali i ne prelaska u potpuno apstraktnu formu.

U Grasshopper-u je istraživanje sprovedeno takođe za tri nivoa iteracija – 3, 5 i 7. Kao i u Python-u, povećanjem broja iteracija raste stepen detaljnosti, dok viši prag homogenosti dovodi do spajanja u veće kvadrate i gubitka detalja. Kod tri iteracije rezultati su vrlo slični onima u Python-u: kvadrati su skoro iste veličine za niže pragove homogenosti, a lik se teško može prepoznati. Međutim, razlike postaju izraženije kod pet iteracija –u Grasshopperu se prepoznatljivost gubi već za granicu homogenosti 10 i lik prelazi u apstraktnu formu. Kod sedam iteracija ovaj efekat je još izraženiji: prepoznatljivost lika nestaje već na pragu od 10, a slika gubi osnovne detalje, iako nije potpuno apstraktan prikaz.
Prema dobijenim rezultatima može se zaključiti da je Python u ovom primjeru generisao postepeniji prelaz između nivoa detalja u zavisnosti od granice prepoznatljivosti, dok je Grasshopper davao grublje podjele.
„Dama sa hermelinom“, Leonardo da Vinči:

U oba alata istraživanje je sprovedeno za tri nivoa iteracija – 4, 6 i 8. Kod četiri iteracije kvalitet prikaza je lošiji: javlja se gruba podjela, međutim prepoznatljivost lika se nazire. Sa šest iteracija struktura postaje jasnija i detaljnija, dok osam iteracija donosi izrazito detaljan rezultat, naročito pri nižim pragovima homogenosti. Međutim, kod vrijednosti praga homogenosti 30 i više dolazi do prekida rekurzivnog dijeljenja već nakon druge rekurzije – pretpostavlja se da je uzrok u jednoličnom koloritu tamne pozadine, gdje algoritam visoku homogenost prepoznaje kao kriterijum za zaustavljanje. Kao rezultat, prepoznatljivost lika prestaje već na pragu homogenosti od 20, jer se detaljno analizira samo polovina, odnosno četvrtina slike.

U Grasshopper-u se uočava slično ponašanje kao i u Python-u. Četvrta iteracija daje prepoznatljive rezultate pri nižim pragovima homogenosti, dok šesta iteracija pruža jasniju strukturu, ali uglavnom pri nižim pragovima homogenosti. Najdetaljniji prikaz javlja se kod osam iteracija, gdje slika poprima izraženu pikselizaciju. Ipak, za sve nivoe iteracija prepoznatljivost lika prestaje već na pragu homogenosti 30. Razlika u odnosu na Python ogleda se u tome što Grasshopper daje ujednačeniju raspodjelu kvadrata, pa je podjela vizuelno skladnija iako gubi detalje u istom rasponu pragova.
Dakle, za ovaj slučaj može se istaći da se oba programa ponašaju slično, ali rezultati u Grasshopperu djeluju ujednačenije i vizuelno skladnije, dok Python pokazuje naglije prelaze i veće razlike u veličini kvadrata.
Zaključak za analizu i komparaciju rezultata: Grasshopper i Python daju lako uporedive rezultate, jer se algoritam rada u ovom slučaju poklapa. Ipak, postoje razlike između njih koje su uočene prilikom ispitivanja različitih slučajeva. Iako je zanemarivo, postoji razlika u vremenskom izvršavanju, odnosno generisanju rezultata. Python, nezavisno od iteracija i granice homogenosti – rezultate daje brže, dok Grasshopper-u treba nešto više vremena za slučaj kad postoji više iteracija – što se u ovom slučaju ne smatra manom jer nisu analizirane previsoke vrijednosti iteracija. Kako se metodologija zasniva na analizi prosječnih vrijednosti piksela, kod slika sa slabijim kolorističkim varijacijama veći prag homogenosti dovodi do gubitka detalja i slabijih rezultata. S obzirom na logiku quadtree strukture, algoritam daje znatno kvalitetnije rezultate u slučajevima bogatijeg kolorita, gdje varijacije u nijansama podstiču dublje rekurzivno dijeljenje.
Analiza prepoznatljivosti
Analiza prepoznatljivosti je bazirana na kombinaciji lične percepcije, koja je dopunjena algoritmima SSIM i PSNR.
PSNR (Peak Signal-to-Noise Ratio) mjeri matematičku razliku intenziteta po pikselima između originalne i obrađene slike izraženu u decibelima. Veće vrijednosti (30 dB i više) ukazuju na veću sličnost, dok niže vrijednosti (ispod 20 dB) ukazuju na manju sličnost.
SSIM (Structural Similarity Index) mjeri koliko se struktura, kontrast i osvijetljenost podudaraju u dvije slike. Vrijednosti bliže 1 ukazuju na veliku sličnost, dok vrijednosti ispod 0.5 znače da je slika vizuelno neprepoznatljiva.

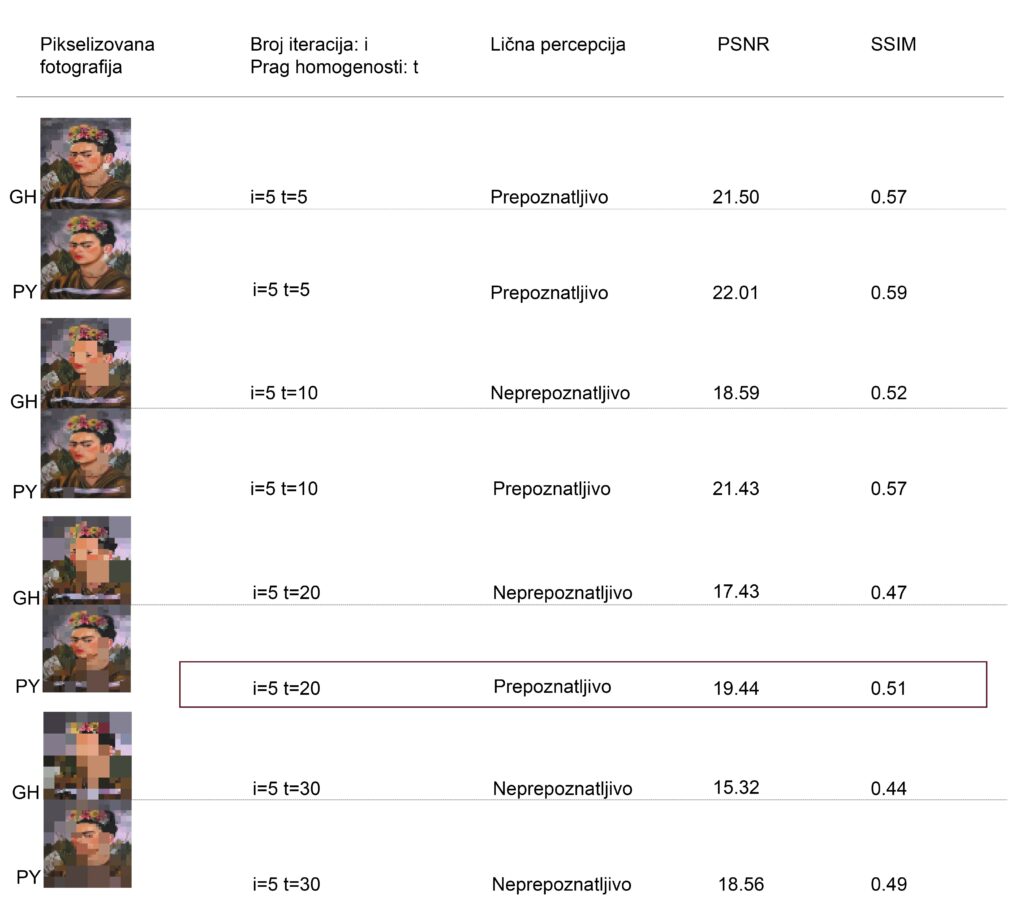

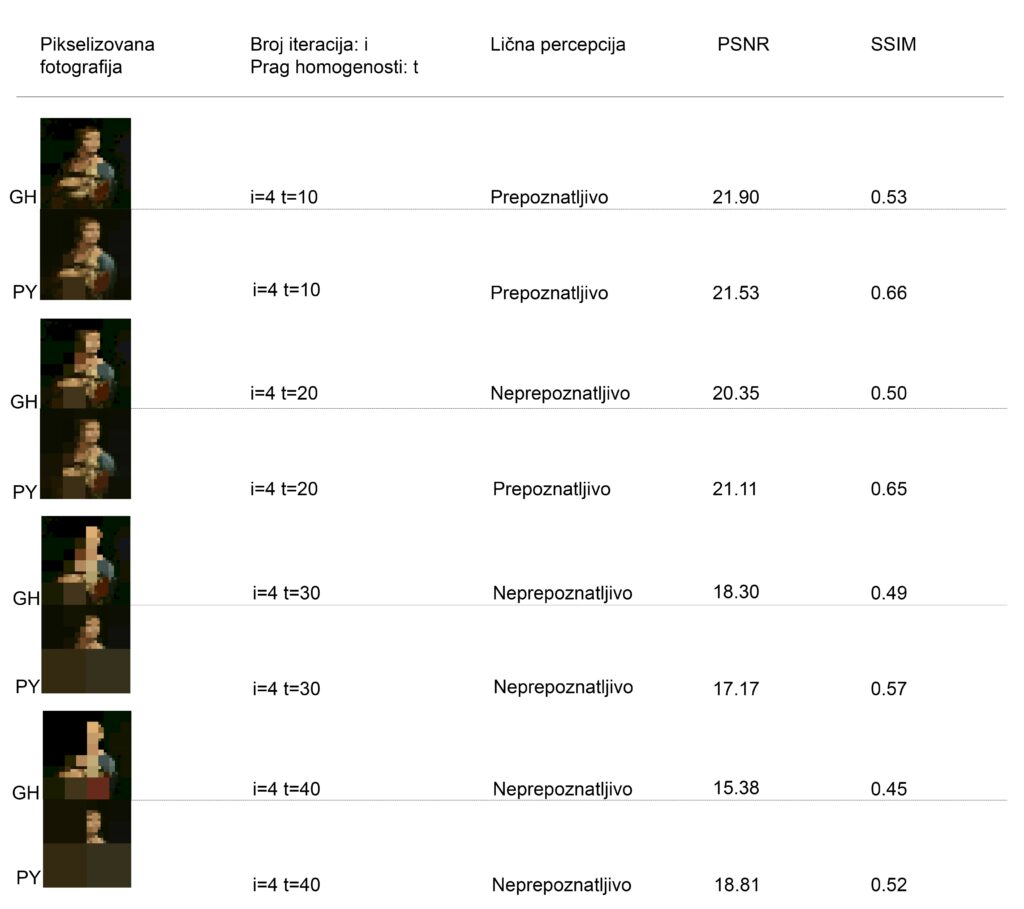
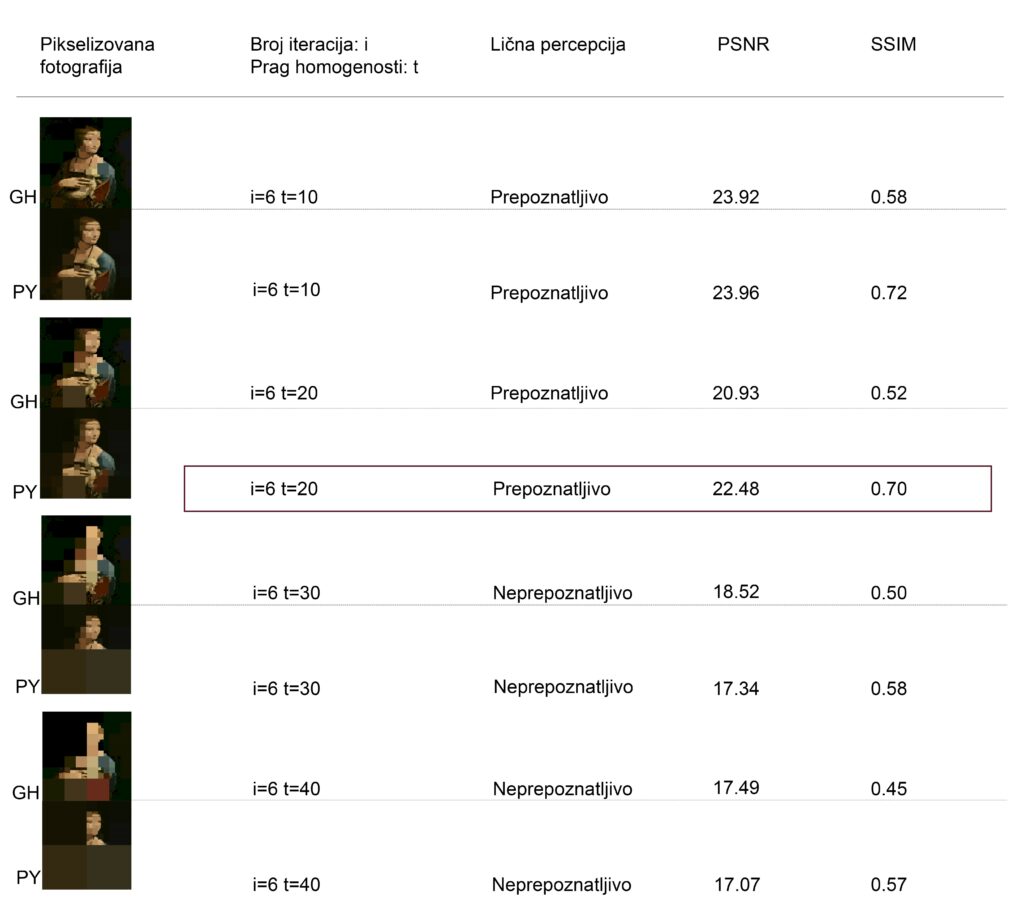

Dobijeni rezultati ne potvrđuju postavljenu hipotezu prema kojoj je granica prepoznatljivosti pretpostavljena na homogenosti 40%. Na osnovu dobijenih rezultata može se zaključiti da repoznatljivost opada za vrijednost praga 30 i više.
Optimalnim rješenjem za autoportret Fride Kalo pokazala se kombinacija i=5 i t=20 (i – broj iteracija; t – granica homogenosti), 1468 kvadrata. Za „Damu sa hermelinom“ optimalna vrijednost dobijena je za i=6 i t=20, sa ukupno 1411 kvadrata. Ovi rezultati su izabrani kao najbolji jer predstavljaju balans između detalja i prepoznatljivosti, slika ostaje dovoljno jasna, a broj kvadrata, odnosno složenost nije prevelika.